Bias Varicne Tradeoff Chinese Version

This Article is a Chinese translation of a study note by Wei. Click here to see the original English version in Wei’s homepage. I will continue to update Chinese translation to sync with Wei’s notes.

请注意: 本文是我翻译的一份学习资料，英文原版请点击Wei的学习笔记。我将不断和原作者的英文笔记同步内容，定期更新和维护。

在这一节中，我们重点讨论偏差和误差之间是如何相互关联的。我们总想拥有0偏差和0方差，然而在实际中这是不可能的。因此，它们之间总会有权衡，一者多，另一者少。

1 偏差-方差间权衡 (Bias Variance Tradeoff)

我们将基于一些样本训练好的模型定义为$\overset{\wedge}{f}$，并且$y$ 为事实标签。因此，均方差(mean squared error(MSE))可以定义为：

\[\mathbb{E}_{(x,y)\sim \text{test set}} \lvert \overset{\wedge}{f}(x) - y \rvert^2\]

对于很高的均方差，我们有以下3种解释：

过渡拟合(overfitting): 模型只在训练样本中表现良好，但是并不能很好地推广适用到测试数据上。

欠拟合(underfitting): 模型训练还不够，或者没有足够的训练数据，以至于模型不能很好的表示训练数据的情况。

两者都不: 数据的噪音(noise)太大。

我们将这些情况归纳为偏差-方差权衡(Bias-Variance Tradeoff)。

假设所有数据都来自于以下定义的相似的分布：$y_i = f(x_i) + \epsilon_i$ 其中噪音 $\mathbb{E}[\epsilon] = 0$ and $Var(\epsilon) = \sigma^2$。

尽管我们的目标是计算f，但我们只能通过从以上分布所产生的样本中训练得到一个估值。因此，$\overset{\wedge}{f}(x_i)$ 是随机的，因为它取决于随机的$\epsilon_i$，并且它也是$y = f(x_i) + \epsilon_i$的预测值。因此，得出$\mathbb{E}(\overset{\wedge}{f}(x)-y)$是很合理的。

我们也可以计算MSE的期望：

\[\begin{align} \mathbb{E}[(y-\overset{\wedge}{f}(x))^2] &= \mathbb{E}[y^2 + (\overset{\wedge}{f})^2 - 2y\overset{\wedge}{f}]\\ &= \mathbb{E}{y^2} + E[(\overset{\wedge}{f})^2] - \mathbb{E}[2y\overset{\wedge}{f}] \\ &= Var(y) + Var(\overset{\wedge}{f}) + (f^2 - 2f\mathbb{E}[\overset{\wedge}{f}] + (\mathbb{E}[\overset{\wedge}{f}])^2\\ &= Var(y) + Var(\overset{\wedge}{f}) + (f - \mathbb{E}[\overset{\wedge}{f}])^2\\ &=\sigma^2 + \text{Bias}(f)^2+ Var(\overset{\wedge}{f}) \end{align}\]

第一项是我们无法处理的噪声。高偏差意味着模型的学习效率很低，并且欠拟合。一个高度的方差代表着模型不能很好的概括更多普通的情况，同时代表过渡拟合。

2 误差分析 (Error Aanalysis)

为了分析一个模型，我们应该首先将模型模块化。然后我们将每个模块的事实标签代入到每一模块中，观察每一个变化会如何影响整体模型的精确度。我们试图观察事实标签中的哪个模块对模型系统的影响最大。以下是一个例子

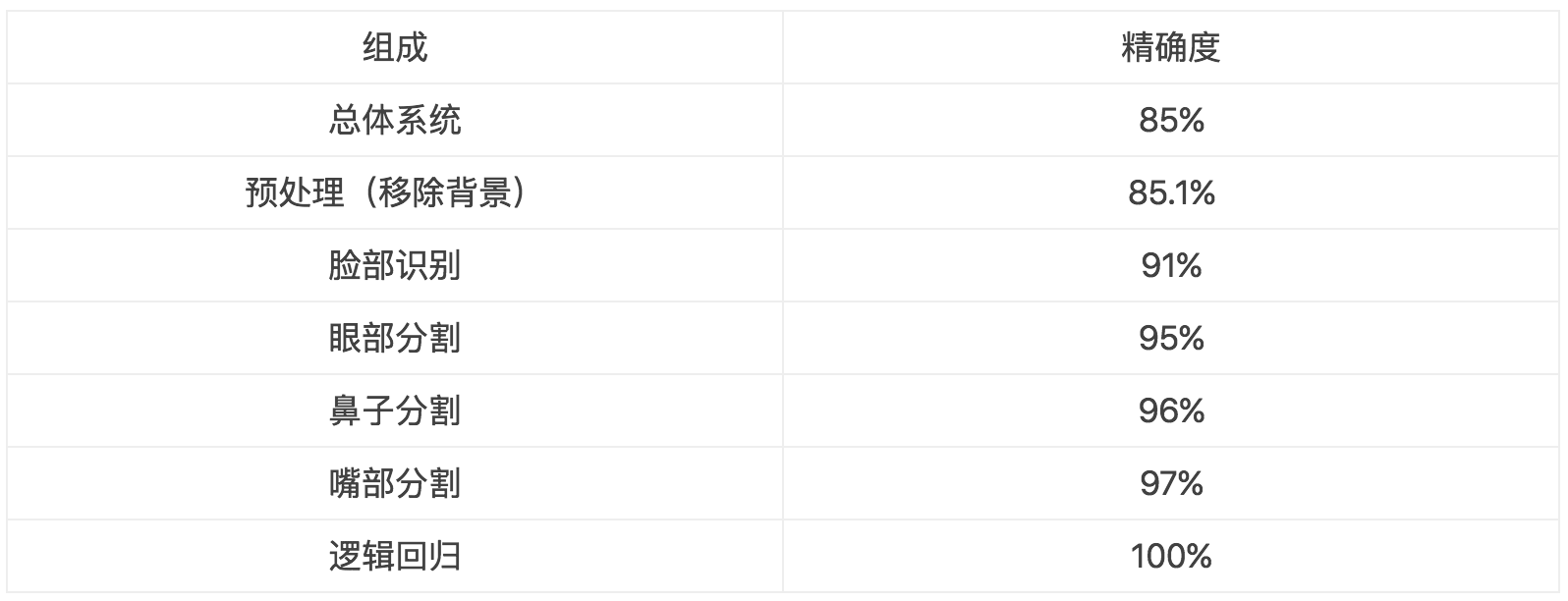
表1：这个表给出了模块化对应的准确度

3 去除分析 (Ablative Analysis)

误差分析试图识别模型当前表现与完美表现之前的区别，而去除分析试图识别基准线与当前模型之前的区别。去除分析非常重要，很多研究论文因为丢失了这部分而被拒绝。这个分析可以告诉我们模型的哪个部分是最具影响力的。 例如，假设我们有更多附加的特征可以让模型表现更好。我们想观察通过每一次减少一个附加的特征，模型的表现会减少多少。下面是一个例子

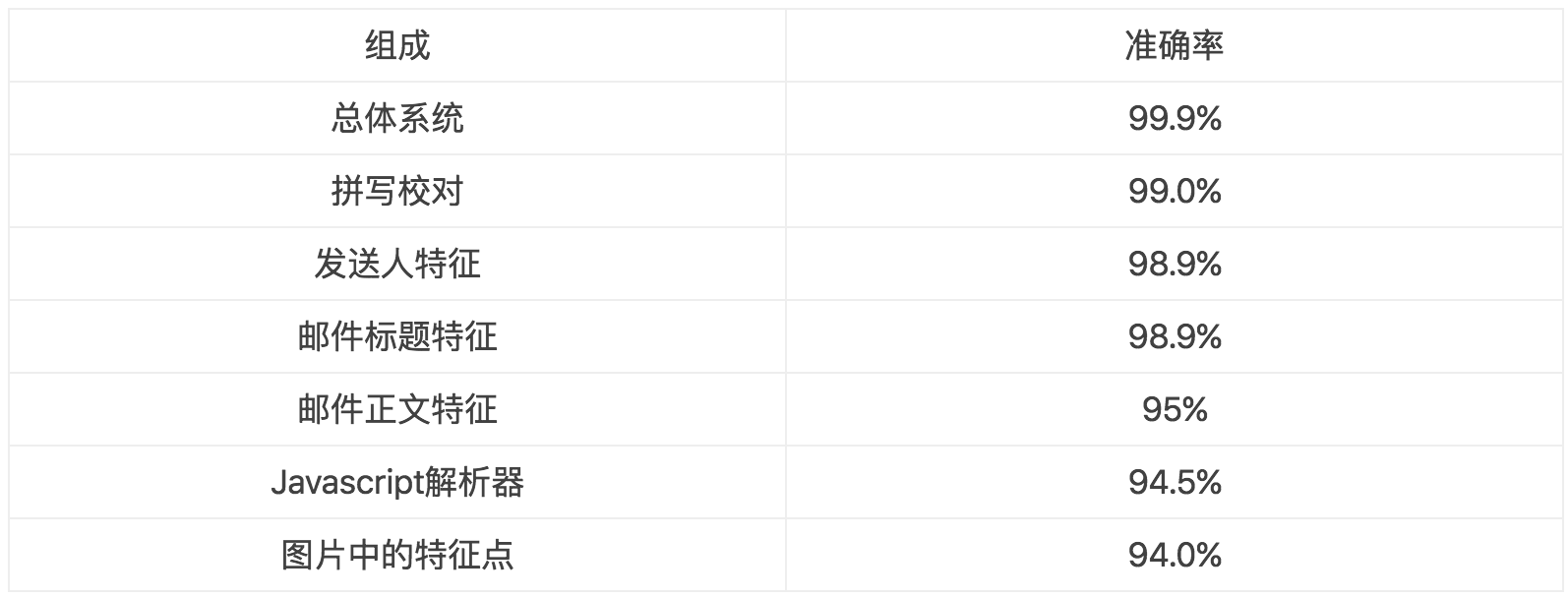
表2：从逻辑回归移除特征的精确度