Discriminative Algorithm Chinese Version

This Article is a Chinese translation of a study note by Wei. Click here to see the original English version in Wei’s homepage. I will continue to update Chinese translation to sync with Wei’s notes.

请注意: 本文是我翻译的一份学习资料，英文原版请点击Wei的学习笔记。我将不断和原作者的英文笔记同步内容，定期更新和维护。

一类经典的学习模式叫做监督学习(supervised learning)。在这种模式下，我们有输入模块，叫特征(features)，和输出模块，叫目标(target)。学习的目的是基于给定的输入和对应的标签训练模型，然后用训练好的模型对给定的新输入来预测输出。

为此，我们收集一个训练数据集(training set)，在这个数据集中，我们有许多成对的训练样本，每对样本包含特征向量(feature vector)作为输入(用符号X表示所有的特征向量)及其相应的目标(output)作为输出（用符号Y表示所有的目标值）。 由于每一个输入都有来自事实对应的标签，我们将这种学习称为监督学习(supervised learning)(有对应标签），同时将训练好的模型称为假设(hypothesis)。 下表是一个例子。

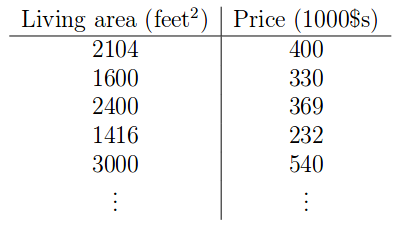
在这种情况下，我们将房子的居住面积作为特征，把价格作为目标。学习任务为给定一个新房子居住面积作为输入，用训练好的模型预测新房子的价格。

当目标输出处于连续空间时，我们将其称为回归问题(regression problem)。 当目标输出处于离散空间时，我们将其称为分类问题(classification problem)。

1 线性回归 Linear Regression

线性回归问题可以通过以下公式来建模：

\[h(x) = \sum\limits_{i=0}^n \theta_i x_i = \theta^Tx\]

我们以 $\theta_0$ 作为偏差项，有时称为截距项。 想象一下，当你尝试回归二维域中的线时，截距项决定了线与y轴交叉的位置。$\theta$ 被称为参数(parameters)，我们将从训练数据中学习它。

为了训练模型，我们定义以下代价函数(cost function)，并试图将它最小化：

\[J(\theta) = \frac{1}{2}\sum\limits_{i=1}^m (h_{\theta}(x^{(i)}) - y^{(i)})^2\]

训练的目的是找到最小化代价的$\theta$。那么如何实现呢？为什么函数前面会有 $\frac{1}{2}$ 呢？在下一节中我们将推导出该成本函数的导数并给出解释。简而言之，这种定义方式使数学运算变得方便。

最小均方算法Least Mean Square(LMS) algorithm

LMS算法主要使用梯度下降(gradient descent)来找到局部最小值(local minimum)。 为了实现它，我们将参数初始化为0，即 $\theta = \overrightarrow{0}$ ，然后用以下方法来反复更新 $\theta$：

\[\theta_j = \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta)\]

其中j可以遍历特征向量中的所有维度。$\alpha$ 被称为学习率(learning rate)，它控制模型学习/训练的速度。这种一步步更新来找到最小值叫迭代算法（iterative algorithm）。

现在，我们根据一个样本求偏导数：

\[\begin{align} \frac{\partial}{\partial \theta_j}J(\theta) &= \frac{\partial}{\partial \theta_j} \frac{1}{2} (h_{\theta}(x)-y)^2\\ &= 2\frac{1}{2}(h_{\theta}(x)-y) \frac{\partial}{\partial \theta_j} (h_{\theta}(x)-y)\\ &= (h_{\theta}(x)-y) \frac{\partial}{\partial \theta_j}(\sum\limits_{i=0}^n \theta_i x_i - y) \\ &= (h_{\theta}(x)-y) x_j \end{align}\]

数学解释：第二行是求导数的链式规则(chain rule)。在第三行，我根据定义扩展 $h_{\theta}(x) = \sum\limits_{i=0}^n \theta_i x_i$ 。 在最后一行，因为我们只关心 $\theta_j$，所以其他一切都是常数。

所以，所有样本的更新是：

\[\theta_j = \theta_j + \alpha\sum\limits_{i=0}^m (y^{(i)} - h_{\theta}(x^{(i)}))x_j^{(i)}\]

其中m是训练样本的数量，j可以跨越特征向量的维度。 该算法从每个训练样本中获取对应梯度信息。 我们称之为批量梯度下降(batch gradient descent)。 该方法对局部最小值(即可能到达的鞍点（saddle point））敏感，而我们通常假设代价函数仅有全局最小值(global minimum)(J是凸函数（convex function）)， 这也是这个例子的情况 。梯度变化如下图所示：

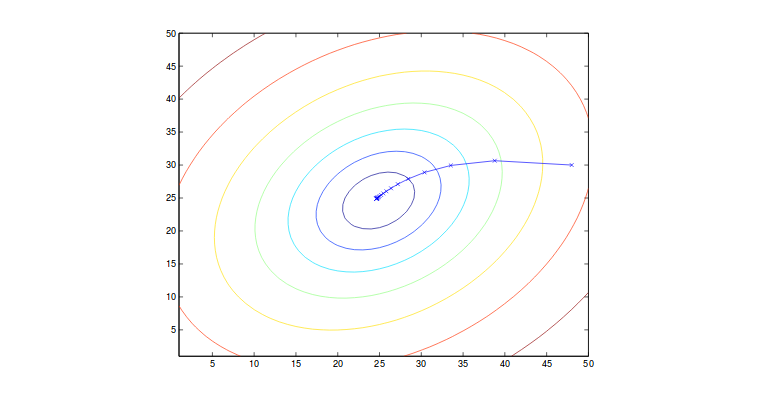
请注意，在更新过程中，我们会遍历所有样本以向局部最小值前进一步。如果m非常大，则该算法每一次迭代计算量十分巨大。 因此，在这种情况下，我们引入了一个类似算法，称为随机梯度下降（stochastic gradient descent）。其中每次算法只会从一小部分样本中计算代价和梯度。 尽管它可能会在最小值处振荡(并没有严格到达最小)，但这样做使模型可以更快收敛。因此，我们经常在现实中使用它。

当不能直接计算或者很难计算使目标函数的导数并设为0的求参数时，我们会用以上的迭代算法。如果可以直接计算使导数为0的参数，我们可以通过下面的正则方程直接计算。

2 正则方程 Normal Equations

回想一下求函数最值的方法，我们可以设函数的导数为0来求得函数的最值，这样我们可以直接地计算局部最小值，而不是通过多次迭代。首先让我们来复习一下数学！

矩阵导数

一些相关概念在其他页面中有所讨论，你可以在这里查看。

在本小节中，我将讨论线性代数中矩阵的迹(trace)的计算，迹被定义为：

\[trA = \sum\limits_{i=1}^n A_{ii}\]

其中A必须是方矩阵。现在我将列出迹的属性和对应证明。

\[trAB = trBA\]

证明：

\[\begin{align} trAB &= \sum\limits_{i=1}^N (AB)_{ii} \\ &= \sum\limits_{i=1}^N \sum\limits_{j=1}^M A_{ij}B_{ji} \\ &= \sum\limits_{j=1}^M \sum\limits_{i=1}^N B_{ji} A_{ij}\\ &= trBA \blacksquare \end{align}\] \[trABC = trCAB = trBCA\]

证明：

\[\begin{align} trABC &= \sum\limits_{i=1}^N (ABC)_{ii} \\ &= \sum\limits_{i=1}^N \sum\limits_{j=1}^M \sum\limits_{p=1}^K A_{ij}B_{jk}C_{ki} \\ &= \sum\limits_{p=1}^K \sum\limits_{i=1}^N \sum\limits_{j=1}^M C_{ki}A_{ij}B_{jk}\\ &= trCAB \blacksquare \end{align}\]

另一个证明类似。 请注意，由于矩阵维度约束，你无法随机调整每个矩阵的顺序。

\[trABCD = trDABC = trCDAB = trBCDA\]

证明:与上面类似

\[trA = trA^T\]

证明:

\[\begin{align} trA &= \sum\limits_{i=1}^N A_{ii} \\ &= \sum\limits_{i=1}^N A_{ii}^T \\ &= trA^T \blacksquare \end{align}\] \[tr(A+B) = trA + trB\]

证明:与上面类似。

\[tr\alpha A = \alpha trA\]

证明:与上面类似。

\[\triangledown_A trAB = B^T\]

证明：

\[\begin{align} \triangledown_{A_ij} trAB &= \sum\limits_{i=1}^N (AB)_{ii} \\ &= \sum\limits_{i=1}^N \sum\limits_{j=1}^M A_{ij} B_{ji} \\ &= B_{ji} \end{align}\]

我们知道：

\[\triangledown_A trAB = \begin{bmatrix} \frac{\partial trAB}{\partial A_{11}} & \frac{\partial trAB}{\partial A_{12}} & \dots & \frac{\partial trAB}{\partial A_{1M} }\\ \frac{\partial trAB}{\partial A_{21} } & \frac{\partial trAB}{\partial A_{22} } & \dots & \frac{\partial trAB}{\partial A_{2M} } \\ \vdots & \vdots & \dots & \vdots \\ \frac{\partial trAB}{\partial A_{N1} } & \frac{\partial trAB}{\partial A_{N2} } & \dots & \frac{\partial trAB}{\partial A_{NM}} \end{bmatrix}\]

带入可得:

\[\triangledown_A trAB = B^T\] \[\triangledown_{A^T}f(A) = (\triangledown_A f(A))^T\]

证明:假设$f:\mathbb{R}^{M\times N}\rightarrow\mathbb{R}$，可得：

\[\begin{align} \triangledown_{A^T} f(A) &= \begin{bmatrix} \frac{\partial f}{\partial (A^T)_{11}} & \frac{\partial f}{\partial (A^T)_{12}} & \dots & \frac{\partial f}{\partial (A^T)_{1M} }\\ \frac{\partial f}{\partial (A^T)_{21} } & \frac{\partial f}{\partial (A^T)_{22} } & \dots & \frac{\partial f}{\partial (A^T)_{2M} } \\ \vdots & \vdots & \dots & \vdots \\ \frac{\partial f}{\partial (A^T)_{N1} } & \frac{\partial f}{\partial (A^T)_{N2} } & \dots & \frac{\partial f}{\partial (A^T)_{NM}} \end{bmatrix} \\ &= \Bigg(\begin{bmatrix} \frac{\partial f}{\partial A_{11}} & \frac{\partial f}{\partial A_{12}} & \dots & \frac{\partial f}{\partial A_{1N} }\\ \frac{\partial f}{\partial A_{21}} & \frac{\partial f}{\partial A_{22} } & \dots & \frac{\partial f}{\partial A_{2N} } \\ \vdots & \vdots & \dots & \vdots \\ \frac{\partial f}{\partial A_{M1} } & \frac{\partial f}{\partial A_{M2} } & \dots & \frac{\partial f}{\partial A_{MN}} \end{bmatrix}\Bigg)^T\\ &= (\triangledown_{A} f(A))^T \blacksquare \end{align}\] \[\triangledown_A trABA^TC = CAB + C^TAB^T\]

证明：trace只存在于方矩阵，，因此可得$A\in\mathbb{R}^{N\times M}，B\in\mathbb{R}^{M\times M}，C\in\mathbb{R}^{N\times N}$

\[\begin{align} \triangledown_A trABA^TC &= \begin{bmatrix} \frac{\partial trABA^TC}{\partial A_{11}} & \frac{\partial trABA^TC}{\partial A_{12}} & \dots & \frac{\partial trABA^TC}{\partial A_{1M} }\\ \frac{\partial trABA^TC}{\partial A_{21}} & \frac{\partial trABA^TC}{\partial A_{22} } & \dots & \frac{\partial trABA^TC}{\partial A_{2M} } \\ \vdots & \vdots & \dots & \vdots \\ \frac{\partial trABA^TC}{\partial A_{N1} } & \frac{\partial trABA^TC}{\partial A_{N2} } & \dots & \frac{\partial trABA^TC}{\partial A_{NM}} \end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial \sum\limits_{i=1}^N(ABA^TC)_{ii}}{\partial A_{11}} & \frac{\partial \sum\limits_{i=1}^N(ABA^TC)_{ii}}{\partial A_{12}} & \dots & \frac{\partial \sum\limits_{i=1}^N(ABA^TC)_{ii}}{\partial A_{1M}}\\ \frac{\partial \sum\limits_{i=1}^N(ABA^TC)_{ii}}{\partial A_{21}} & \frac{\partial \sum\limits_{i=1}^N(ABA^TC)_{ii}}{\partial A_{22} } & \dots & \frac{\partial \sum\limits_{i=1}^N(ABA^TC)_{ii}}{\partial A_{2M} } \\ \vdots & \vdots & \dots & \vdots \\ \frac{\partial \sum\limits_{i=1}^N(ABA^TC)_{ii}}{\partial A_{N1} } & \frac{\partial \sum\limits_{i=1}^N(ABA^TC)_{ii}}{\partial A_{N2} } & \dots & \frac{\partial \sum\limits_{i=1}^N(ABA^TC)_{ii}}{\partial A_{NM}} \end{bmatrix} \end{align}\] \[= \begin{bmatrix} \frac{\partial \sum\limits_{i=j=k=h=1}^{N，M，M，N} A_{ij}B_{jk}A_{hk}C_{hi}}{\partial A_{11}} & \frac{\partial \sum\limits_{i=j=k=h=1}^{N，M，M，N} A_{ij}B_{jk}A_{hk}C_{hi}}{\partial A_{12}} & \dots & \frac{\partial \sum\limits_{i=j=k=h=1}^{N，M，M，N} A_{ij}B_{jk}A_{hk}C_{hi}}{\partial A_{1M}}\\ \frac{\partial \sum\limits_{i=j=k=h=1}^{N，M，M，N} A_{ij}B_{jk}A_{hk}C_{hi}}{\partial A_{21}} & \frac{\partial \sum\limits_{i=j=k=h=1}^{N，M，M，N} A_{ij}B_{jk}A_{hk}C_{hi}}{\partial A_{22} } & \dots & \frac{\partial \sum\limits_{i=j=k=h=1}^{N，M，M，N} A_{ij}B_{jk}A_{hk}C_{hi}}{\partial A_{2M} } \\ \vdots & \vdots & \dots & \vdots \\ \frac{\partial \sum\limits_{i=j=k=h=1}^{N，M，M，N} A_{ij}B_{jk}A_{hk}C_{hi}}{\partial A_{N1} } & \frac{\partial \sum\limits_{i=j=k=h=1}^{N，M，M，N} A_{ij}B_{jk}A_{hk}C_{hi}}{\partial A_{N2} } & \dots & \frac{\partial \sum\limits_{i=j=k=h=1}^{N，M，M，N} A_{ij}B_{jk}A_{hk}C_{hi}}{\partial A_{NM}} \end{bmatrix}\] \[=\begin{bmatrix} \dots & \sum\limits_{k，h}^{M，N} B_{Mk}A_{hk}C_{h1} + \sum\limits_{i，j}^{N，M} A_{ij}B_{jM}C_{1i}\\ \dots & \sum\limits_{k，h}^{M，N} B_{Mk}A_{hk}C_{h2} + \sum\limits_{i，j}^{N，M} A_{ij}B_{jM}C_{2i} \\ \dots & \vdots \\ \dots & \sum\limits_{k，h}^{M，N} B_{Mk}A_{hk}C_{hN} + \sum\limits_{i，j}^{N，M} A_{ij}B_{jM}C_{Ni} \end{bmatrix}\] \[= C^TAB^T + CAB\] \[\triangledown_A \lvert A \rvert = \lvert A \rvert(A^{-1})^T\]

再看Least Square

因此，现在我们不是迭代地找到解决方案，而是明确地直接计算代价函数对于 $\theta$ 的导数，并将其设为零以便直接解出最终表达式。

我们定义训练集输入为：

\[X = \begin{bmatrix} -(x^{(1)})^T-\\ -(x^{(2)})^T- \\ \vdots \\ -(x^{(m)})^T- \end{bmatrix}\]

输出为:

\[\overrightarrow{y} = \begin{bmatrix} y^{(1)}\\ y^{(2)} \\ \vdots \\ y^{(m)} \end{bmatrix}\]

定义模型为 $h_{\theta}(x^{(i)}) = (x^{(i)})^T\theta$，我们得到:

\[X\theta - \overrightarrow{y} = \begin{bmatrix} h_{\theta}(x^{(1)}) - y^{(1)}\\ h_{\theta}(x^{(2)}) - y^{(2)} \\ \vdots \\ h_{\theta}(x^{(m)}) - y^{(m)} \end{bmatrix}\]

因此，

\[J(\theta) = \frac{1}{2}(X\theta - \overrightarrow{y})^T(X\theta - \overrightarrow{y}) = \frac{1}{2}\sum\limits_{i=1}^m (h_{\theta}(x^{(i)}) - y^{(i)})^2\]

现在我们需要找到J对于 $\theta$ 的导数。 从矩阵的迹的属性来看，我们知道：

\[\triangledown_{A^T}trABA^TC = B^TA^TC^T + BA^TC\]

我们知道标量的迹是它自己，因此:

\[\begin{align} \triangledown_{\theta}J(\theta) &= \triangledown_{\theta}\frac{1}{2}(X\theta - \overrightarrow{y})^T(X\theta - \overrightarrow{y})\\ &= \frac{1}{2}\triangledown_{\theta} tr(\theta^TX^TX\theta - \theta^TX^T\overrightarrow{y} - \overrightarrow{y}^TX\theta + \overrightarrow{y}^T\overrightarrow{y}) \\ &= \frac{1}{2}\triangledown_{\theta} (tr\theta^TX^TX\theta - 2tr\overrightarrow{y}^TX\theta)\\ &= \frac{1}{2}(X^TX\theta + X^TX\theta - 2X^T\overrightarrow{y})\\ &= X^X\theta - X^T\overrightarrow{y} \end{align}\]

数学解释：标量$a = tr(a)$，因此可得第二行。第三行（1）对$\overrightarrow{y}^T\overrightarrow{y}$求$\theta$导可得0；（2）$tr(A+B) = tr(A) + tr(B)$;(3) $- \theta^TX^T\overrightarrow{y} - \overrightarrow{y}^TX\theta = 2\overrightarrow{y}^TX\theta$；。第四行来源于(1)使用之前的迹的性质，其中$A^T = \theta，B = B^T = X^TX， C = I$;(2)$\triangledown_A trAB = B^T$.

我们将它设为0，可得正则方程，即：

\[X^TX\theta = X^T\overrightarrow{y}\]

因此我们可算出使矩阵导数为0的$\theta$为:

\[\theta = (X^TX)^{-1}X^T\overrightarrow{y}\]

3 概率解释

正则方程是找到解的一种确定性方法，让我们看看如何从随机性的角度解释它。随机性解释下最终应该得到相同的结果。

我们知道输入和输出的关系为：

\[y^{(i)} = \theta^Tx^{(i)} + \epsilon^{(i)}\]

其中 $\epsilon^{(i)}$ 是随机变量，它捕获噪声和非模型的因素。 这通常是线性回归的概率模型。 我们还假设噪声是独立同分布(i.i.d.)，并来自高斯分布，该分部有均值为 $\theta$ 和任意方差 $\sigma^2$ ，这是一种传统的线性回归建模方式。 $\epsilon^{(i)}$ 是高斯的随机变量，并且 $\theta^T x^{(i)}$ 对于这个随机变量来说是常数。 向高斯随机变量添加常数将使该变量的均值移动常数数量，但它仍然是高斯分布，只是具有不同的均值和相同的方差。因此，按照高斯分布的定义，我们可以说：

\[p(y^{(i)} \lvert x^{(i)};\theta) = \frac{1}{\sqrt{2\pi}\sigma}\exp\big(-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}\big)\]

当x已知并具有固定参数$\theta$时，该函数可被视为y的函数。 因此，我们可以称之为似然函数likelihood function：

\[L(\theta) = \prod_{i=1}^{m} p(y^{(i)} \lvert x^{(i)};\theta)\]

我们需要找到满足以下条件的$\theta$：选定 $\theta$ 的情况下，基于给定x，y的概率要最大化。 我们称之为最大似然法。 为简化，我们来找最大对数似然(log likelihood)：

\[\begin{align} \ell &= \log L(\theta)\\ &= \log \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\sigma}\exp\big(-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}\big)\\ &= \sum\limits_{i=1}^{m} \log \frac{1}{\sqrt{2\pi}\sigma}\exp\big(-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}\big)\\ &= m\log\frac{1}{\sqrt{2\pi}\sigma} - \frac{1}{\sigma^2}\frac{1}{2}\sum\limits_{i=1}^{m}(y^{(i)} - \theta^T x^{(i)})^2 \end{align}\]

对于 $\theta$ 来最大化以上值会与最小化代价函数得到相同的答案。这意味着我们用概率的方式证明了我们在最小均方算法中所得的结果。

4 局部加权线性回归

在上面讨论的回归方法中，我们平等对待在每个训练样本产生的代价。 但是每个样本所带来的代价是不一样的，尤其是一些异常值(outlier)会增加很多代价,我们应该减少它们权重。因此我们根据查询点(querying point)来计算每个样本的权重。 例如，这样的权重可以是：

\[w^{(i)} = \exp\big(-\frac{(x^{(i)} - x)^2}{2r^2}\big)\]

虽然这个表达式看似于高斯，但它们无关。 x是查询点。 我们需要保留所有训练数据以进行新的预测。

5 分类与逻辑回归

我们可以将分类问题当做一个特殊的回归问题，我们只回归到一组二进制值0和1。有时，我们也使用-1和1表示法，我们分别称它为负类和正类。

然而，如果我们在这里应用线性回归模型，那么我们预测0和1以外的任何值是没有意义的。因此，我们将假设函数修改为：

\[h_{\theta}(x) = g(\theta^T x) = \frac{1}{1+\exp(-\theta^Tx)}\]

其中g称为逻辑函数或sigmoid函数，如图所示：

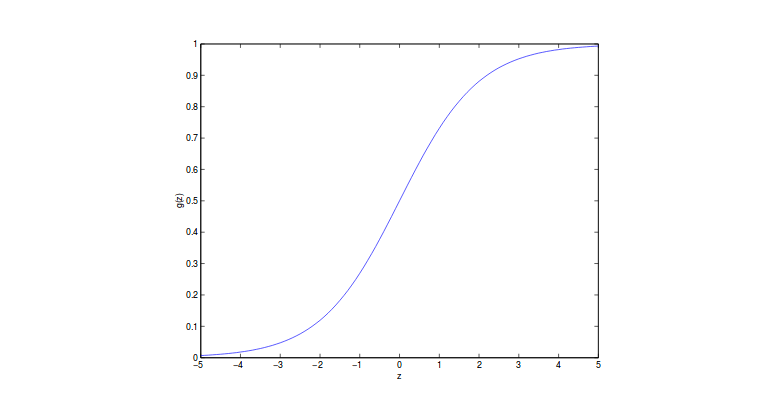
输出范围从0到1。这直观地解释了为什么我们将其称为回归，因为它在连续的空间中输出。 但是，该值表示属于某一类的概率。 所以基本上它是一个分类器。

让我们来看看逻辑函数的导数会是什么：

\[\begin{align} \frac{d}{dz} g(z) &= \frac{1}{(1+\exp(-z))^2}\big(\exp(-z)\big)\\ &= \frac{1 + \exp(-z) - 1}{(1+\exp(-z))^2} \\ &= \frac{1}{(1+\exp(-z))}\Big(1 - \frac{1}{1+\exp(-z)}\Big)\\ &= g(z)(1-g(z)) \end{align}\]

有了这个知识，接下来的问题是如何找到 $\theta$。 我们知道最小二乘回归可以从最大似然算法中计算出，我们从这里继续。

我们认为：

\[P(y \lvert x;\theta) = (h_{\theta}(x))^y (1 - h_{\theta}(x))^{1-y}\]

其中y应为1或0。 假设样本是独立同分布，我们有似然函数：

\[\begin{align} L(\theta) &= \prod_{i=1}^{m} p(y^{(i)}\lvert x^{(i)};\theta)\\ &= \prod_{i=1}^{m} (h_{\theta}(x^{(i)}))^{y^{(i)}} (1 - h_{\theta}(x^{(i)}))^{1-y^{(i)}} \end{align}\]

使用log函数，可得:

\[\log L(\theta) = \sum\limits_{i=1}^m y^{(i)}\log h(x^{(i)}) + (1-y^{(i)})\log(1-h(x^{(i)})\]

然后，我们可以使用梯度下降来优化代价函数。 在更新中，我们应该有 $\theta = \theta + \alpha\triangledown_{\theta}L(\theta)$。 注意我们有加号而不是减号，因为我们发现最大值不是最小值。 接下来求导数：

\[\begin{align} \frac{\partial}{\partial\theta_j}L(\theta) &= \bigg(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(^Tx)}\bigg)\frac{\partial}{\partial\theta_j}g(\theta^Tx)\\ &= \bigg(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(^Tx)}\bigg) g(\theta^Tx)* \\ &(1 - g(\theta^Tx))\frac{\partial}{\partial\theta_j}\theta^Tx\\ &= (y - h_{\theta}(x))x_j \end{align}\]

从第一行到第二行，我们使用上面导出的逻辑函数的导数。 这为我们提供了特征向量上每个维度的更新规则。 虽然在这种情况下我们有与LMS相同的算法，但在这种情况下的假设函数是不同的。 当我们谈论广义线性化模型时，使用相同的等式并不是偶然。

6 插话：感知器学习算法

我们在之后的学习理论中会继续讨论，简单来讲，我们把假设函数调整为：

\[g(\theta^Tx) = \begin{cases} 1 \text{， if } \theta^Tx \geq 0 \\ 0 \text{， otherwise} \\ \end{cases}\]

之前的更新方程保持不变，这就是感知器学习算法。

7 牛顿最大化方法

想象一下，我们想要找到函数f的根。 牛顿法允许我们以二次速度完成这项任务。 这个想法是：随机初始化 $x_0$ 并找到 $f(x_0)$ 的切线，标记为$f^{\prime}(x_0)$。 我们使用 $f^{\prime}(x_0)$ 的根作为新x。 我们还将新x和旧x之间的距离定义为 $\Delta$ 。 下图可以展示这个过程：

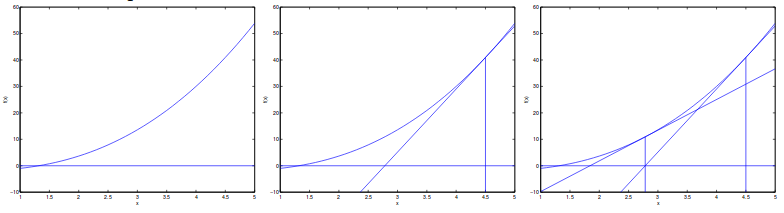
所以我们得到：

\[f^{\prime}(x_0) = \frac{f(x_0)}{\Delta} \Rightarrow \Delta = \frac{f(x_0)}{f^{\prime}(x_0)}\]

从这个想法得出，我们可以让 $f(x) = L^{\prime}(\theta)$。 通过这种方式，我们可以更快地找到目标函数的最大值。 为了找到最小值的方法类似。

如果 $\theta$ 是矢量值，我们需要在更新中使用海森矩阵(Hessian matrix)。 关于海森矩阵的更多细节可以在[另一篇文章]中找到(https://wei2624.github.io/Useful-Formulas-for-Math/)。 简而言之，为了更新，我们有：

\[\theta = \theta - H^{-1}\triangledown_{\theta}L(\theta)\]

虽然它也可以二次收敛，但是计算起来可比梯度下降麻烦得多。

8 广义线性模型和指数族

在我们更新逻辑回归和最小均方回归时形式一样，这看似巧合。主要是因为它们是大家族广义线性模型中的特殊情况。 它被称为线性的原因是该族中的每个分布中的变量和它们的权重之间存在线性关系。

在进入广义线性模型之前，我们讨论指数族分布作为它的基础。 如果可以以下面的形式来表示一个分布，我们定义在指数族中的一类分布：

\[p(y;\eta) = b(y)\exp(\eta^T T(y) - a(\eta))\]

其中$\eta$ 称为自然参数，$T(y)$ 称为充分统计量，而$a(\eta)$称为对数分割函数。 通常，我们的情况里，$T(y) = y$。$-a(\eta)$ 是归一化常数。

T，a和b是固定参数，我们可以通过改变 $\eta$ 来建立不同的分布。 现在，我们可以证伯努利分布和高斯分布属于指数族:

伯努利：

\[\begin{align} p(y;\phi) &= \phi^y(1-\phi)^{1-y}\\ &= \exp(y\log\phi + (1-y)\log(1-\phi))\\ &= \exp\bigg(\bigg(\log\bigg(\frac{\phi}{1-\phi}\bigg)\bigg)y+\log(1-\phi)\bigg) \end{align}\]

其中:

\[\eta = \log(\phi/(1-\phi))\] \[T(y) = y\] \[a(\eta) = -\log(1-\phi) = \log(1+e^{\eta})\] \[b(y) = 1\]

高斯：

\[p(y;\mu) = \frac{1}{\sqrt{2\pi}}\exp\bigg(-\frac{1}{2}y^2\bigg)\exp\bigg(\mu y - \frac{1}{2}\mu^2\bigg)\]

其中 $\sigma$ 是1，我们仍然可以变化 $\sigma$ 以及以下参数：

\[\eta = \mu\] \[T(y) = y\] \[a(\eta) = \mu^2/2 = \eta^2/2\] \[b(y) = (1/\sqrt{2\pi})\exp(-y^2/2)\]

其他指数分布：多项分布，泊松分布，伽马分布和指数分布，贝塔分布和狄利克雷分布。 由于它们都处于指数族，我们能做的是研究一般形式的指数族，并改变 $\eta$ 以建立不同的模型。

9 构建广义线性模型

如上所述，一旦我们知道了T，a和b，就已经确定了分布族。 我们只需要找到 $\eta$ 来确定确切的分布。

例如，假设我们想要基于给定的x预测y。 在继续推导出这个回归问题的构建广义线性模型之前，我们对此做出三个主要假设：

(1)我们总是假设 $y \lvert x;\theta \thicksim \text{ExponentialFamily}(\eta)$.

(2)通常，我们想要预测给定x的T（y）的期望值。 最有可能的是，我们有 $T(y) = y$。定义上，我们有 $h(x) = \mathbb{E}[y\lvert x]$，这对于逻辑回归和线性回归都是正确的。 注意，在逻辑回归中，我们总是有 $\mathbb{E}[y\lvert x] = p(y=1\lvert x;\theta)$

(3)输入和自然参数关联为：$\eta = \theta^Tx$

9.1普通最小二乘法

在这种情况下，我们有 $y\thicksim \mathcal{N}(\mu，\sigma^2)$。 以前，我们讨论过高斯作为指数族。 特别是，我们有：

\[\begin{align} h_{\theta}(x) &= \mathbb{E}[y\lvert x;\theta]\\ &= \mu\\ &= \eta \\ &=\theta^Tx \end{align}\]

其中第一个等式来自假设（2）; 第二个是定义; 第三个来自之前的推导; 最后一个是假设（3）。

9.2 逻辑回归

在此设置中，我们预测类标签为1或0。 回想一下，在伯努利中，我们有 $\phi=1/(1+e^{\eta})$ 。因此，我们可以推导出以下等式：

\[\begin{align} h_{\theta}(x) &= \mathbb{E}[y\lvert x;\theta]\\ &= \phi\\ &= 1/(1+e^{-\eta}) \\ &= 1/(1+e^{-\theta^Tx}) \end{align}\]

这部分解释了为什么我们得出了sigmoid函数这样的形式。 因为我们假设当给定x，y是伯努利分布，所以由指数族来产生sigmoid函数是很自然的事。 为了预测，我们认为 $T(y)$ 是相对于 $\eta$ 的期望值合理的猜测，即规范响应函数或链接函数的反函数

。 通常，响应函数是 $\eta$ 的函数，并给出 $\eta$ 和分布参数之间的关系，而链接函数产生η作为分布参数的函数。 反函数意味着用一者来表达另一者。 从上面的推导，我们知道伯努利的响应函数是逻辑函数，而高斯函数的典型响应函数是均值函数。

9.3 Softmax回归

在更广泛的情况下，我们可以有多个类而不是上面的二项类。 将其建模为多项分布是很自然的，它也属于可以从广义线性模型导出的指数族。

在多项分布中，我们可以将 $\phi_1，\phi_2，\dots，\phi_{k-1}$ 定义为 $k-1$ 类的对应概率。 我们不需要所有k类，因为一旦设置了前一个k-1就确定了最后一类。 所以我们可以写为 $\phi_k = 1-\sum_{i=1}^{k-1}\phi_i$

我们首先定义 $T(y) \in \mathbb{R}^{k-1}$，并且：

\[T(1) = \begin{bmatrix} 1\\ 0 \\ \vdots \\ 0 \end{bmatrix}， T(2) = \begin{bmatrix} 0\\ 1 \\ \vdots \\ 0 \end{bmatrix}，\dots，T(k) = \begin{bmatrix} 0\\ 0 \\ \vdots \\ 0 \end{bmatrix}\]

注意，对于 $T(k)$，我们在向量中只有全零，因为向量的长度是k-1。 我们让 $T(y)_i$ 来定义在向量中的第i个元素。 课程笔记说明中也引入了指标的定义，我在此不再详述。

现在，我们展示了将多项式推导为指数族的步骤：

\[\begin{align} p(y;\phi) &= \phi_1^{\mathbb{1}[y=1]}\phi_2^{\mathbb{1}[y=2]}\dots\phi_k^{\mathbb{1}[y=k]}\\ &= \phi_1^{\mathbb{1}[y=1]}\phi_2^{\mathbb{1}[y=2]}\dots\phi_k^{1 - \sum_{i=1}^{k-1}\mathbb{1}[y=i]}\\ &= \phi_1^{T(y)_1}\phi_2^{T(y)_2}\dots\phi_k^{1 - \sum_{i=1}^{k-1}T(y)_i} \\ &= \exp\Big(T(y)_1\log(\phi_1/\phi_k)+T(y)_2\log(\phi_2/\phi_k) + \dots \\ &+ T(y)_{k-1}\log(\phi_{k-1}/\phi_k)+ \log(\phi_k)\Big) \\ &= b(y)\exp(\eta^TT(y) - a(\eta)) \end{align}\]

其中

\[\eta = \begin{bmatrix} \log(\phi_1/\phi_k)\\ \log(\phi_2/\phi_k) \\ \vdots \\ \log(\phi_{k-1}/\phi_k) \end{bmatrix}\]

并且，

$a(\eta) = -\log(\phi_k)$ and $b(y) = 1$

这将多项式表示为指数族。 我们现在可以将链接函数视为：

\[\eta_i = \log(\frac{\phi_i}{\phi_k})\]

为了得到响应函数，我们改变链式函数：

\[e^{\eta_i} = \frac{\phi_i}{\phi_k}\] \[\phi_k e^{\eta_i} = \phi_i\] \[\phi_k \sum\limits_{i=1}^{k}e^{\eta_i} = \sum\limits_{i=1}^{k} \phi_i\]

因此我们得到响应函数为：

\[\phi_i = \frac{e^{\eta_i}}{\sum_{j=1}^{k}e^{\eta_j}}\]

这个响应函数就是我们的softmax函数。

根据广义线性模型中的假设（3），我们知道对于对于$i=1，2，\dots，k-1$， $\eta_i = \theta_i^Tx$ ，并且 $\theta_i \in \mathbb{R}^{n+1}$ 是我们广义线性模型模型的参数。而 $\theta_k$ 只是0，因此 $\eta_k = 0$ 。 现在，我们有基于x的模型：

\[p(y=i\lvert x;\theta) = \phi_i = \frac{e^{\eta_i}}{\sum_{j=1}^{k}e^{\eta_j}} = \frac{e^{\theta_i^T x}}{\sum_{j=1}^{k}e^{\theta_j^Tx}}\]

这个模型就叫做softmax回归，是逻辑回归的广泛形式。因此，假设函数成为：

\[\begin{align} h_{\theta}(x) &= \mathbb{E}[T(y)\lvert x;\theta]\\ &=\begin{bmatrix} \phi_1\\ \phi_2 \\ \vdots \\ \phi_{k-1} \end{bmatrix} \\ &= \begin{bmatrix} \frac{\exp(\theta_1^Tx)}{\sum_{j=1}^k\exp(\theta_j^Tx)}\\ \frac{\exp(\theta_2^Tx)}{\sum_{j=1}^k\exp(\theta_j^Tx)} \\ \vdots \\ \frac{\exp(\theta_{k-1}^Tx)}{\sum_{j=1}^k\exp(\theta_j^Tx)} \end{bmatrix} \end{align}\]

现在，我们需要优化$\theta$来最大化log似然函数，根据定义，我们可以写为：

\[\begin{align} L(\theta) &= \sum\limits_{i=1}^m \log(p(y^{(i)}\lvert x^{(i)};\theta)\\ &=\sum\limits_{i=1}^m \log\prod_{l=1}^k\bigg(\frac{\exp(\theta_l^Tx)}{\sum_{j=1}^k\exp(\theta_j^Tx)}\bigg)^{\mathbb{1}\{y^{(i)}=l\}} \end{align}\]

我们可以用梯度下降或者牛顿方法来找到最大值。

记住：逻辑回归是softmax回归的二项形式。sigmoid函数是softmax函数的二项形式。