Generative Learning Algorithm in Chinese
Please note this post is a study note translated to Chinese by me. Click here to see the original English version in Wei’s homepage.
请注意: 本文是我翻译的一份学习资料,英文原版请点击Wei的学习笔记。
生成学习算法
1 判别模型
判别模型是一种对观测数据进行直接分类的模型,常见的模型有逻辑回归和感知机学习算法等。此模型仅对数据进行分类,并不能具象化或者量化数据本身的分布状态,因此也无法根据分类生成可观测的图像。
定义上,判别模型通过构建条件概率分布p(y|x;θ)预测y,即在特征x出现的情况下标记y出现的概率。此处p可以是逻辑回归模型。
2 生成模型
与判别模型不同,生成模型首先了解数据本身分布情况,并进一步根据输入x,给出预测分类y的概率。该模型有着研究数据分布形态的概念,可以根据历史数据生成新的可观测图像。
而贝叶斯分类就是一个典型的例子。在这个例子中,我们首先有一个先验分类。这个先验的分布其实就是我们对数据分布的一个假设(如高斯分布,二项分布或多项分布),我们假设我们选择的模型可以正确解释数据集中的隐含信息。从数据集中,我们可以知道哪些参数最适合我们选择的模型。在这个已计算出先验概率的模型中,我们可以使用贝叶斯公式来进一步计算每个类的概率,然后挑出较大的概率供我们使用。与此同时,给定任意一个先验概率分布,我们可以根据这个分布生成新的样本y,进而基于所选择的先验生成新的特征x(比如,基于一个患癌症的先验概率与分布,我们可以生成新的患病者特征x)。这就是所谓的生成过程。
3 高斯判别分析
高斯判别分析(GDA)是一个生成模型,其中p(x|y)是多元高斯正态分布。
3.1 多元高斯正态分布
在多元正态分布中,一个随机变量是一个$R^n$空间中的矢量值,其中n代表维度数。因此,多元高斯的均值向量 μ∈$R^n$,协方差矩阵Σ∈$R^n$ ,其中Σ是对称的半正定矩阵。其概率密度函数为:
\[p(x;\mu,\Sigma) = \frac{1}{(2\pi)^{n/2}\lvert \Sigma\rvert^{1/2}}\exp\bigg(-\frac{1}{2}(x - \mu)^T\Sigma^{-1}(x - \mu)\bigg)\]如上所述,μ代表期望值。
随机向量Z(或者说,向量化的随机变量Z)的协方差为:
\[\begin{align} Cov(Z) &= E[(Z-E[Z])(Z-E[Z])^T] \\ &= E[ZZ^T - 2ZE[Z]^T + E[Z]E[Z]^T]\\ &= E[ZZ^T] - 2E[Z]E[Z]^T + E[Z]E[Z]^T\\ &=E[ZZ^T] - E[Z]E[Z]^T \end{align}\]下图显示了几个密度函数,它们的均值均为零,但协方差不同:
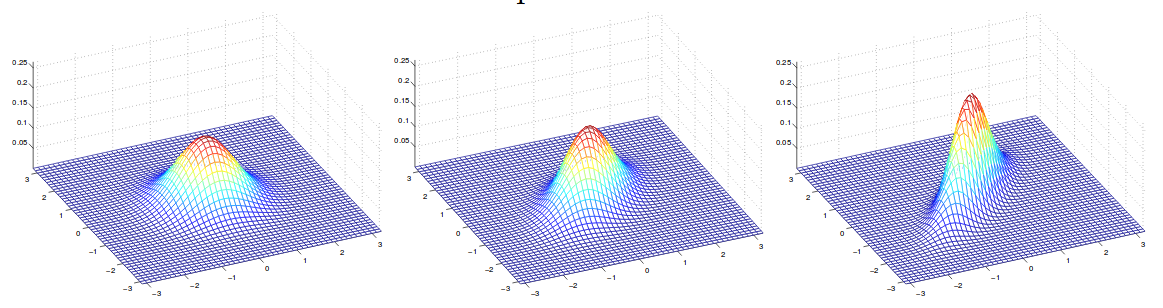
上图的协方差为(从左到右):
\[\Sigma = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}; \Sigma = \begin{bmatrix} 1 & 0.5 \\ 0.5 & 1 \end{bmatrix}; \Sigma = \begin{bmatrix} 1 & 0.8 \\ 0.8 & 1 \end{bmatrix}\]4 高斯判别分析和逻辑回归
4.1 高斯判别分析
我们再来谈谈二分类问题,我们可以用多元高斯模型对p(x|y)进行建模。 总的来讲,我们有:
\[y \sim Bernoulli(\phi)\] \[x\lvert y=0 \sim \mathcal{N}(\mu_0,\Sigma)\] \[x\lvert y=1 \sim \mathcal{N}(\mu_1,\Sigma)\]在这里面,我们想要找出的参数φ,μ0,μ1,和Σ。 请注意,虽然每个类的均值不同,但它们的协方差相同。
这里有人会问,那为什么它是一个生成模型呢?简而言之,我们首先有一个类,也有这个类的y的先验概率分布,并且知道这个类的分布类型是伯努利分布。那么生成过程就是(1)从伯努利分布的类中抽样。 (2)基于类标签,我们从相应的分布中抽取x。这便是一个生成过程。
所以,该数据的对数似然函数值为:
\[\begin{align} \ell(\phi,\mu_0,\mu_1,\Sigma) &= \log \prod_{i=1}^m p(x^{(i)}, y^{(i)};\phi,\mu_0,\mu_1,\Sigma) \\ &= \log \prod_{i=1}^m p(x^{(i)}\lvert y^{(i)};\mu_0,\mu_1,\Sigma) p(y^{(i)};\phi)\\ &= \sum\limits_{i=1}^m \log p(x^{(i)}\lvert y^{(i)};\mu_0,\mu_1,\Sigma) p(y^{(i)};\phi) \end{align}\]在上面的等式中,我们插入每个分布,但不指明具体这个分布是哪个类,我们仅将它们抽象为k。我们可以得到:
\[\begin{align} \ell(\phi,\mu_k,\Sigma) &= \sum\limits_{i=1}^m \log p(x^{(i)}\lvert y^{(i)};\mu_k,\Sigma) p(y^{(i)};\phi)\\ &= \sum\limits_{i=1}^m \bigg[-\frac{n}{2}\log 2\pi-\frac{1}{2}\log\lvert\Sigma\rvert \\ &-\frac{1}{2}(x^i-\mu_k)^T\Sigma^{-1}(x^i-\mu_k)\\ & + y^i\log\phi+(1-y^i)\log(1-\phi)\bigg]\\ \end{align}\]现在,我们需要对每个参数进行取导,然后将它们设为零并找到 argmax(函数值最大时对应的输入值x)。 一些可能对推导有用的公式列举如下:
\(\frac{\partial x^TAx}{\partial x} = 2x^TA\) iff A is symmetric and independent of x
证明: 矩阵A是对称矩阵,所以 A= AT并假设空间维度为n。
\[\begin{align} \frac{\partial x^TAx}{\partial x} &= \begin{bmatrix} \frac{\partial x^TAx}{\partial x_{1}} \\ \frac{\partial x^TAx}{\partial x_{2}} \\ \vdots \\ \frac{\partial x^TAx}{\partial x_{n}}\end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial \sum\limits_{i=1}^n\sum\limits_{j=1}^n x_iA_{ij}x_j }{\partial x_{1}} \\ \frac{\partial \sum\limits_{i=1}^n\sum\limits_{j=1}^n x_iA_{ij}x_j}{\partial x_{2}} \\ \vdots \\ \frac{\partial \sum\limits_{i=1}^n\sum\limits_{j=1}^n x_iA_{ij}x_j}{\partial x_{n}} \end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial \sum\limits_{i=1}^n A_{i1}x_i +\sum\limits_{j=1}^n A_{1j}x_j }{\partial x_{1}} \\ \frac{\partial \sum\limits_{i=1}^n A_{i2}x_i +\sum\limits_{j=1}^n A_{2j}x_j}{\partial x_{2}} \\ \vdots \\ \frac{\partial \sum\limits_{i=1}^n A_{in}x_i +\sum\limits_{j=1}^n A_{nj}x_j}{\partial x_{n}} \end{bmatrix} \\ &= (A + A^T)x \\ &= 2x^TA \blacksquare \end{align}\] \[\frac{\partial \log\lvert X\rvert}{\partial X} = X^{-T}\]雅可比公式:
\[\frac{\partial \lvert X\rvert}{X_{ij}} = adj^T(X)_{ij}\]证明:
\[\begin{align} \frac{\partial \log\lvert X\rvert}{\partial X}&=\frac{1}{\lvert X\rvert} \frac{\partial \lvert X\rvert}{\partial X} \\ &= \frac{1}{\lvert X\rvert} * adj^T (X)_{ij} \\ &= \frac{1}{\lvert X^T\rvert} * adj^T (X)_{ij} \\ &= X^{-T} \blacksquare \end{align}\] \[\frac{\partial a^TX^{-1}b}{\partial X} = -X^{-T}ab^TX^{-T}\]证明:
这个证明有些复杂。你应该事先了解克罗内克函数和Frobenius内部乘积。对于矩阵X,我们可以写成:
\[\frac{\partial X_{ij}}{\partial X_{kl}} = \delta_{ik}\delta{jl} = \mathcal{H}_{ijkl}\]你可以将H视为Frobenius内积的标识元素。在开始证明之前,让我们准备好去找逆矩阵的导数。也就是说,∂X-1/∂X。
\[\begin{align} I^{\prime} &= (XX^{-1})^{\prime} \\ &= X^{\prime}X^{-1} + X(X^{-1})^{\prime} \\ &= 0 \end{align}\]所以我们可以这么解:
\[X(X^{-1})^{\prime} = -X^{\prime}X^{-1} \rightarrow (X^{-1})^{\prime} = X^{-1}X^{\prime}X^{-1}\]接着,让我们回到正题:
\[\begin{align} a^TX^{-1}b &= \sum\limits_{i,j=1}^{n,n} a_ib_j(X^{-1})_{ij} \\ &= \sum\limits_{i,j=1}^{n,n} (ab^T)_{ij}(X^{-1})_{ij} \\ &= \sum\limits_{i,j=1}^{n,n} ((ab^T)^T)_{ji}(X^{-1})_{ij} \\ &= tr(ab^T\cdot X^{-1}) \\ &= < ab^T, X^{-1}>_F \end{align}\]其中F表示Frobenius内积。
接着,带回到原始公式:
\[\begin{align} \frac{\partial a^TX^{-1}b}{\partial X} &= \frac{\partial < ab^T, X^{-1} >_F}{\partial X} \\ &= < ab^T, \frac{\partial X^{-1}}{X} >_F \\ &= < ab^T, \frac{\partial X^{-1}}{X} >_F \\ &= < ab^T, X^{-1}X^{\prime}X^{-1} >_F \\ &= < ab^T, (X^{-T})^T X^{\prime}(X^{-T})^T >_F \\ &= < X^{-T}ab^TX^{-T},X^{\prime} >_F \\ &= < X^{-T}ab^TX^{-T},\mathcal{H} >_F \\ &= X^{-T}ab^TX^{-T} \blacksquare \end{align}\]现在,我们已经有足够的准备去找到每个参数的梯度了。
对ϕ取导并设为0:
\[\begin{align} \frac{\partial \ell(\phi,\mu_k,\Sigma)}{\partial \phi} &= \sum\limits_{i=1}^m (-0-0+0+\frac{y^i}{\phi}-\frac{1-y^i}{1-\phi})=0\\ &\Rightarrow \sum\limits_{i=1}^m y^i(1-\phi)-(1-y^i)\phi = 0\\ &\Rightarrow \sum\limits_{i=1}^m y^i -m\phi = 0\\ &\Rightarrow \phi = \frac{1}{m}\sum\limits_{i=1}^m \mathbb{1}\{y^{(i)}=1\} \end{align}\]对 μk取导并设为0:
\[\begin{align} \frac{\partial \ell(\phi,\mu_k,\Sigma)}{\partial \mu_k} &= \sum\limits_{i=1}^m (-0-0-\frac{1}{2}2(x_k^i-\mu_k)^T\Sigma^{-1}\mathbb{1}\{y^i=k\})=0\\ &\Rightarrow \sum\limits_{i=1}^m x_k^i\mathbb{1}\{y^i=k\} - \mu_k \mathbb{1}\{y^i=k\} = 0\\ &\Rightarrow \mu_0 = \frac{\sum_{i=1}^m\mathbb{1}\{y^{(i)}=0\}x^{(i)}}{\sum_{i=1}^m\mathbb{1}\{y^{(i)}=0\}}\\ &\Rightarrow \mu_1 = \frac{\sum_{i=1}^m\mathbb{1}\{y^{(i)}=1\}x^{(i)}}{\sum_{i=1}^m\mathbb{1}\{y^{(i)}=1\}} \end{align}\]对 Σ 取导并设为0:
\[\begin{align} \frac{\partial \ell(\phi,\mu_k,\Sigma)}{\partial \Sigma} &= \sum\limits_{i=1}^m (-\frac{1}{2}\Sigma^{-T}-\frac{1}{2} (\Sigma^{-T}(x_k^i-\mu_k)(x_k^i-\mu_k)^T\Sigma^{-T}))=0\\ &\Rightarrow \sum\limits_{i=1}^m (1-\Sigma^{-T}(x_k^i-\mu_k)(x_k^i-\mu_k)^T) = 0\\ &\Rightarrow m - \sum\limits_{i=1}^m \Sigma^{-T}(x_k^i-\mu_k)(x_k^i-\mu_k)^T = 0\\ &\Rightarrow m\Sigma = \sum\limits_{i=1}^m (x_k^i-\mu_k)(x_k^i-\mu_k)^T\\ &\Rightarrow \Sigma = \frac{1}{m}\sum\limits_{i=1}^m (x^{(i)} - \mu_{y^{(i)}})(x^{(i)} - \mu_{y^{(i)}})^T \end{align}\]结果如图所示:
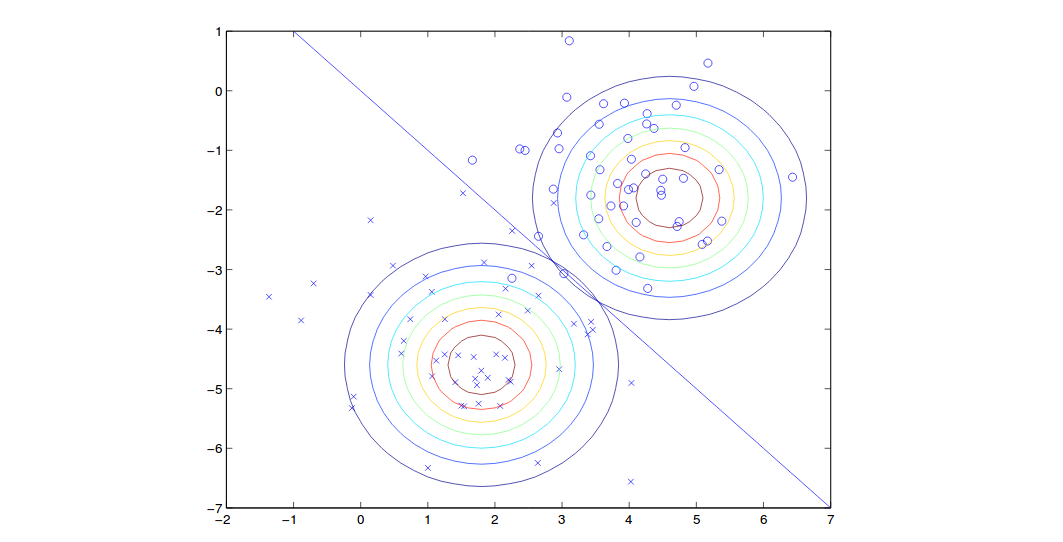
请注意,由于有着同样的协方差,因此上图两个轮廓的形状是相同的,然而均值不同。在边界线这条线上(自左上到右下的直线),每个类的概率为50%。
4.2 高斯判别分析(GDA)和逻辑回归
高斯判别分析又是如何与逻辑回归相关联的呢?我们可以发现如果上述p(x|y) 是具有共同协方差的多元高斯,我们就可以计算p(x|y)并证明它是遵循逻辑函数的。要证明这一点,我们可以:
\[p(y=1\lvert x;\phi,\mu_0,\mu_1,\Sigma) = \frac{p(x,y=1,;\phi,\mu_0,\mu_1,\Sigma)}{p(x;\phi,\mu_0,\mu_1,\Sigma)}\] \[\begin{align} &=\frac{p(y=1\lvert x;\phi)p(x\lvert \mu_1,\Sigma)}{p(y=1\lvert x;\phi)p(x\lvert \mu_1,\Sigma) + p(y=0\lvert x;\phi)p(x\lvert \mu_0,\Sigma)} \\ &= \frac{\phi\mathcal{N}(x\lvert \mu_1,\Sigma)}{\phi\mathcal{N}(x\lvert \mu_1,\Sigma) + (1- \phi)\mathcal{N}(x\lvert \mu_0,\Sigma)} \\ &= \frac{1}{1 + \frac{(1- \phi)\mathcal{N}(x\lvert \mu_0,\Sigma)}{\phi\mathcal{N}(x\lvert \mu_1,\Sigma)}} \\ \end{align}\]由于高斯属于指数族,我们最终可以将分母中的比率转换为exp(θTx),其中 θ 是φ,μ0,μ1,Σ的函数。
同样的,如果p(x|y) 是具有不同 λ 的泊松分布,则p(x|y) 也遵循逻辑函数。 这意味着GDA模型本身有一个强假设,即每个类的数据都可以用具有共享协方差的高斯模型建模。但是,如果这个假设是正确的话,GDA将可以更好并且更快地训练模型。
另一方面,如果不能做出假设,逻辑回归就不那么敏感了。因此,你可以直接使用逻辑回归,而无需接触高斯假设或泊松假设。
5 朴素贝叶斯
在高斯判别分析中,随机变量应使用具有连续值特征的数据。 而朴素贝叶斯则用于学习离散值随机变量,如文本分类。在文本分类中,模型基于文本中的单词将文本标记为二进制类,单词被向量化并用于模型训练。一个单词向量就像一本字典一样,其长度是字典中单词储存的数量,其二进度值则代表着是否为某个词。 一个单词在单词向量中由1表示“存在”,由0表示不存在这个单词。
比方说,一个Email的向量可以表示为:
\[x = \begin{bmatrix} 1 \\ 1 \\ 0 \\ \vdots \\ 1 \\ \vdots \end{bmatrix}\]其中前两个词可以是“运动”和“篮球” 。(因为原著大佬很喜欢打篮球,所以这里他用了运动和篮球作为例子…)
然而,这可能并不起作用。比方说,如果我们有50000个单词(len(x) = 50000)并尝试将其建模为多项分布。定义上讲,我们可以对$p(x\lvert y)$建模,其中p为多项分布。由于每个单词都只有两个状态,要么存在要么不存在,这就是二元情况。对于多项分布,我们必须对所有可能性进行建模,这意味着类的数量将会是一封邮件中所有可能结果的总和。这种情况下,对于给定的类,每个单词既可以是独立的,也可以是非独立的,这并不要紧。要紧的是我们将其建模为多项分布后,参数的维数将会是$2^{50000}-1$,这实在是太大了。因此,为了解决这个问题,我们做出了朴素贝叶斯假设:
在朴素贝叶斯假设中 - 基于给定分类,每个词彼此之间条件独立。
具体来说,如果我们有一封已被标记为“运动”分类的邮件,则“篮球”一词的出现与“扣篮”一词的出现相互独立。基于以上假设,我们可以独立地对每个单词进行建模,我们可以将它建模为伯努利分布。当然,我们知道这个假设也许是错误的,这也是它之所以被称Naive的原因(Naive是朴素贝叶斯中朴素的英文,它也有天真的、无知的、幼稚的意思)。但根据我的个人经验,朴素贝叶斯将给你提供相当不错的结果。如果你打算删除此假设的话,你需要对数据依赖性进行大量的额外计算。
所以,我们有:
\[\begin{align} P(x_1,...,x_{50000}\lvert y) &=P(x_1\lvert y)P(x_2\lvert y,x_1)\\ &...P(x_{50000}\lvert y,x_1,x_2,...,x_{49999}) \\ &=\prod\limits_{i=1}^{n} P(x_i\lvert y) \end{align}\]我们对第一步应用概率论中的链式法则,对第二步应用朴素贝叶斯假设。
找到对数似然函数值的最大值:
\[\begin{align} \mathcal{L}(\phi_y,\phi_{j\lvert y=0},\phi_{j\lvert y=1}) &= \prod\limits_{i=1}^{m} P(x^{(i)},y^{(i)}) \\ &=\prod\limits_{i=1}^{m} P(x^{(i)} \lvert y^{(i)}) P(y^{(i)}) \end{align}\]其中 ϕ j|y=1 = P(xj=1|y=1), ϕj|y=0 = P(xj=1|y=0) 并且 ϕy= p(y=1)。 这些是我们需要训练的参数。
我们可以对其求导:
\[\begin{align} \phi_{j\lvert y=1} &= \frac{\sum_{i=1}^m \mathbb{1}\{x_j^i = 1 \text{and} y^i = 1\}}{\sum_{i=1}^m \mathbb{1}\{y^i = 1\}} \\ \phi_{j\lvert y=0} &= \frac{\sum_{i=1}^m \mathbb{1}\{x_j^i = 1 \text{and} y^i = 0\}}{\sum_{i=1}^m \mathbb{1}\{y^i = 0\}} \\ \phi_y &= \frac{\sum_{i=1}^m \mathbb{1}\{y^i = 1\}}{m} \\ \end{align}\]现在来看,由于每个给定的类学习了50000个参数,参数的总数量大约为100000。这已经比以前少太多了。
为了预测新样本,我们可以使用贝叶斯法则来计算P(y = 1 | x)并比较哪个更高。
\[p(y=1\lvert x) = \frac{p(x\lvert y=1)p(y=1)}{p(x)}\] \[=\frac{p(y=1)\prod_{j=1}^n p(x_j\lvert y=1)}{p(y=0)\prod_{j=1}^n p(x_j\lvert y=0) + p(y=1)\prod_{j=1}^n p(x_j\lvert y=1)}\]延伸: 在这种情况下,因为y是二进制值(0,1),我们将P(xi | y)建模为伯努利分布。 也就是说,它可以是“有那个词”或“没有那个词”。 伯努利将类标签作为输入并对其概率进行建模,前提是它必须是二进制的。 如果是处理非二进制值Xi,我们可以将其建模为多项式分布,多项式分布可以对多个类进行参数化。
总结: 朴素贝叶斯适用于离散空间,高斯判别分析适用于连续空间。我们任何时候都能将其离散化。
6 拉普拉斯平滑处理
上面的示例通常是好的,不过当新邮件中出现过去训练样本中不存在的单词时,该模型将会预测失败。 在这种情况下,它会因为模型从未看到过这个词而导致两个类的φ变为零,以至于无法进行预测。
这时我们则需要另一个解决方案,其名为拉普拉斯平滑,它将每个参数设置为:
\[\begin{align} \phi_{j\lvert y=1} &= \frac{\sum_{i=1}^m \mathbb{1}\{x_j^i = 1 \text{and} y^i = 1\}+1}{\sum_{i=1}^m \mathbb{1}\{y^i = 1\}+2} \\ \phi_{j\lvert y=0} &= \frac{\sum_{i=1}^m \mathbb{1}\{x_j^i = 1 \text{and} y^i = 0\}+1}{\sum_{i=1}^m \mathbb{1}\{y^i = 0\}+2} \\ \phi_j &= \frac{\sum_{i=1}^{m} \mathbb{1}[z^{(i)}] + 1}{m+k} \\ \end{align}\]其中k是类的数量。在实际操作中,拉普拉斯平滑并没有太大的区别,因为我们的模型中通常包含了所有的单词。不过有个Plan B总是极好的~
