Decision Trees
Introduction
Decision tree is one of the most popular non-linear framework used in the reality. It is known for its robustness to noisy and the capability of learning disjunctive expressions. In reality, decision tree has been widely used in credit risk of loan applicants.
A decision tree maps input $x\in \mathbb{R}^d$ to output y using binary rules. From top-down point of view, each node in the tree has a splitting rule. At the very bottom, each leaf node outputs an value or a class. Note, outputs can repeat. Each splitting rule can be characterized as :
\[h(x) = \mathbb{1}[x_j > t]\]for some dimension j and $t\in \mathbb{R}$. From the leaf nodes, we can know the predictions. An example of such a decision tree can be visualized below:
Decision Trees Types
Similar to traditional prediction models, decision trees can be grouped as classification trees and regression trees. Classification trees are to classify input, while regression trees are to regress a real value in the domain as output.
Regression Trees
In this case, you can imagine that we are partitioning the space so that we can make a prediction. As an example, we have a 2 dimensional input space. We can partition each dimension individually and give a regressed value for certain region. You can visualize the idea in the left figure below.
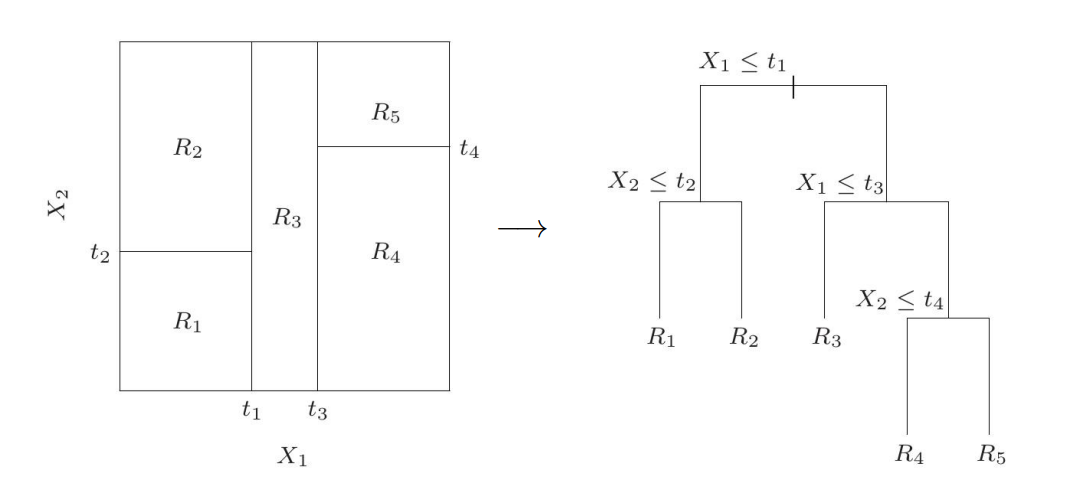
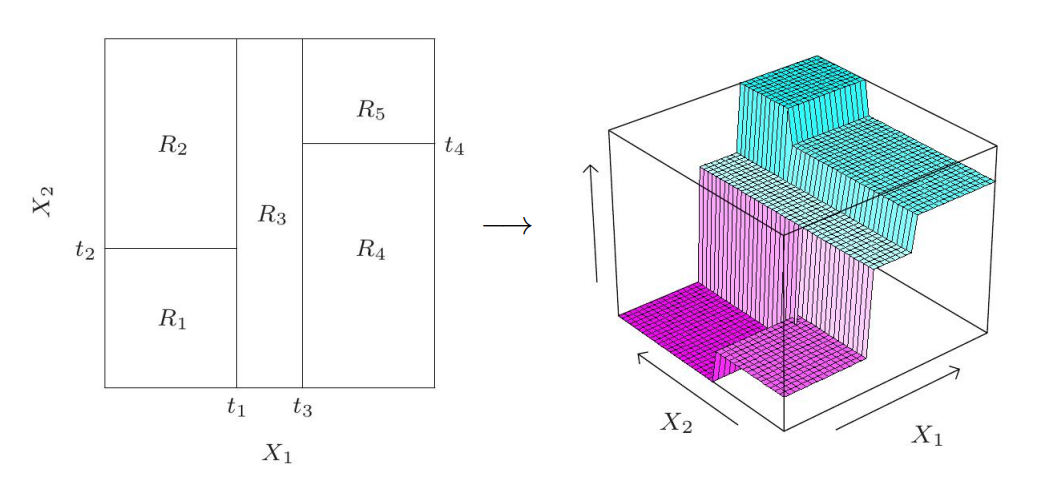
It turns out to be a tree structure such as the right one in the figure above. To predict, we assign $R_1,R_2,R_3,R_4,R_5$ to their corresponding path. In 3D space, we can see the above regression trees can lead to a stair-like partition in 3D.
Classification Trees
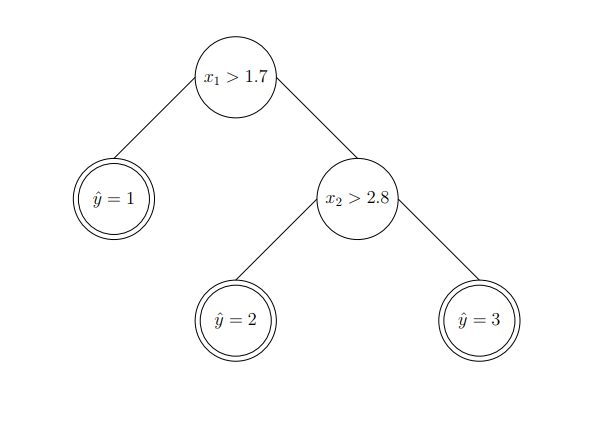
Let’s see an example of this type of decision tree. Say we have two features $x_1,x_2$ as input and 3 class labels as output. Formally, $x \in \mathbb{R}^2$ and $y \in {1,2,3}$. Figuratively, we can see:
Now, we can start from the first feature. Say we choose 1.7 as the threshold value to split. As a result,we can have:
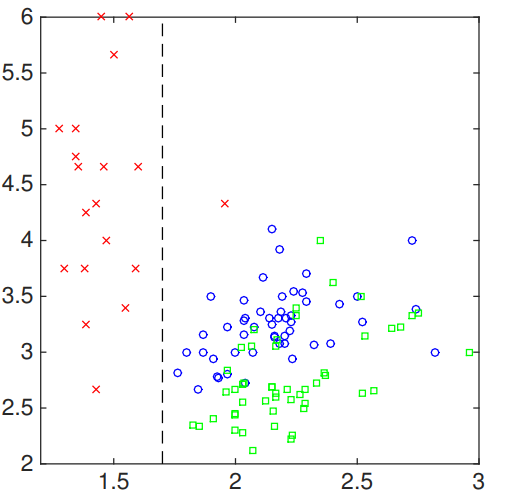
The resulted decision tree can be described as:
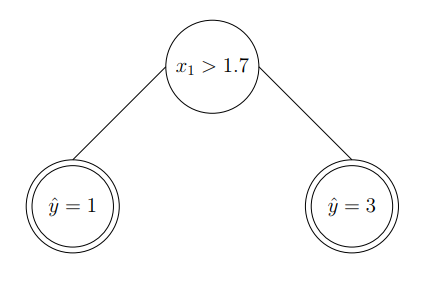
We can perform a similar action to the second feature of input. In particular, we select another threshold value along second feature space, which results in:
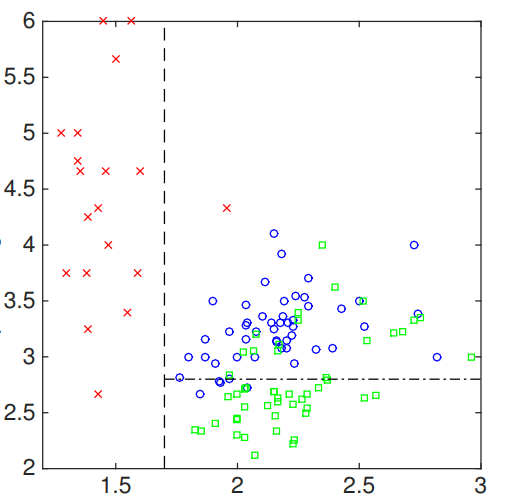
The resulted tree can be visualized as:
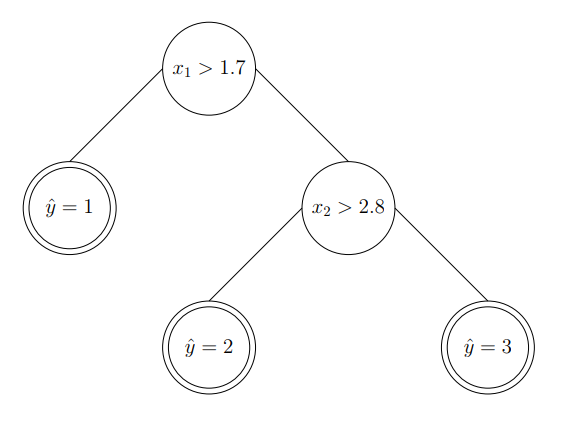
The steps above show the work flow of constructing a classification decision tree from the input space.
Learning Decision Tree
In this section, we are talking about how to learn a decision tree for both types. In general, learning trees is using a top-down greedy algorithm. In this algorithm, we start from a single node. Then, we find out the threshold value which can reduce the uncertainty the most. We keep doing this until all rules are found out.
Learning a Regression Tree
Back to the example:

In the left figure, we have five regions, two input features and four thresholds. Let’s generalize to M regions $R_1,\dots,R_M$. The prediction function can be:
\[f(x) = \sum\limits_{m=1}^M c_m \mathbb{1} \{x\in R_m \}\]where $R_m$ is the region that x belongs to and $c_m$ is the prediction value.
The goal is to minimize:
\[\sum\limits_i (y_i - f(x_i))^2\]Let’s look at this definition. There are two variables that need to be determined, $c_m, R_m$. The prediction is from $c_m$. So if we are given $R_m$, can we make the prediction of $c_m$ easier? The answer is yes. We can simply average all the samples in the region as $c_m$. Now, the question is how do we find out the regions?
Let’s consider to split a reigon R at the splitting value s of dimension j. The intial region is usually the entire dataset. We can define $R^{-}(j,s) = { x_i\in\mathbb{R}^d\lvert x_i(j) \leq s }$ and $R^{+}(j,s) = { x_i\in\mathbb{R}^d\lvert x_i(j) \geq s }$. Then, for each dimension j, we calculate the splitting point s that can achieve the goal the best. We should do this for each existing regirons(leaf node) so far and pick up the best region splitting based on a predefined metric.
In a word, we always select a region (leafnode), then a feature and then a threshold to form a new split.
Learning a classification decision tree.
In regression task, we use a square error to determine the splitting rule. In classification task, we have more options to achieve this.